Bestimmung der Konstruktionswasserlinie

Zur Bestimmung der Konstruktionswasserlinie:

Der Begriff der „Konstruktionswasserlinie“ (KWL) wird im englischen Schiffsbau „unserer“ Zeit nicht verwendet. Man spricht gemeinhin von Wasserlinien. Diese Linien beschreiben je nach Beladung des Schiffs die Höhe der Wasseroberfläche parallel zum Kiel.[i]

Ist das Schiff voll beladen, so verdrängt dieses so viel Wasser, das es bis zur Last-/ Konstruktionswasserlinie eintaucht. Ausgehend von den üblichen Rißzeichnungen (Sheer Draughts/ Plan of Elevation) entspricht dies der Load-Water Line (LWL).

Wird das Schiff (gleichmäßig) geleichtert, so ergibt sich hieraus eine zweite, dritte, usw., zur ersten parallel verlaufende Linie, die um die Höhe des verringerten Gewichts näher am Kiel liegt.[ii] Der Tiefgang (draught) ergibt sich durch die von Eigen- und zugeladenem Gewicht (Displacement, = Rumpf, Kanonen, Mannschaft, Proviant,…) verursachte Verdrängung.

Interessant erscheint in diesem Zusammenhang, daß Blaise Ollivier in seinem Bericht von 1737 über den Vergleich der Schiffsbaukunst zwischen Frankreich, England und Holland die englischen Konstrukteure wegen ihres Mangels an wissenschaftlicher Arbeitsweise rügt. So bemängelt er etwa, daß das Displacement während der Entwurfsphase nicht berechnet wird, während diese Methode in Frankreich mittlerweile berücksichtigt würde.[iii]

Die Bestimmung des Displacements und die Umrechnung in Kubikmeter bzw. –feet ist ein Kapitel für sich und bleibt der einschlägigen Literatur vorbehalten.

Mit Hilfe einer Curve of Displacement läßt sich auf einfache Weise der Tiefgang mittschiffs anhand des vorgesehenen Gewichts ableiten (s. Abb. 1.).[iv]

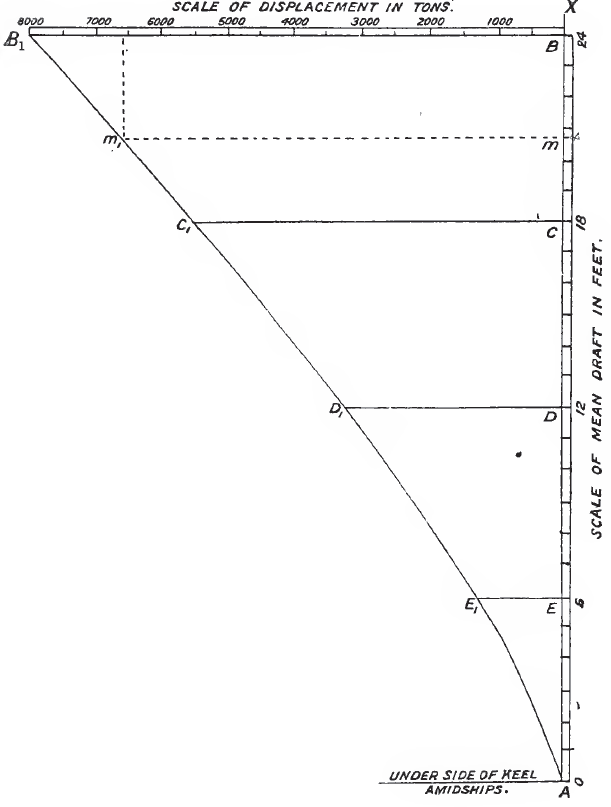
Scale of Displacement

Abbildung 1

Entscheidend für die Konstruktion eines Kriegsschiffes des 18. Jahrhunderts ist und bleibt die Länge des Batteriedecks. Die Länge wird durch die Anzahl der Geschütze auf dem untersten (ca. 4-5 feet über der Load-Water Line liegenden) Deck bestimmt und ist folgendermaßen definiert:

„Die Länge zwischen den Perpendikeln ist in den meisten Kriegsschiffen die Länge des Geschütz- bzw. Unterdecks, gemessen vom Ende der Sponung des Vorderstevens bis zum Beginn der Sponung des Achterstevens auf Höhe des Unterdecks.“[v]

Die genaue Kenntnis der Deckslänge ist für die weiteren Berechnungen in der Konstruktion unerläßlich und nicht mit anderen Längenangaben (Kiellänge, Länge über alles, Keel for Tonnage) zu verwechseln.

Zur Konstruktion bzw. Berechnung von Körpern sind neben der Länge weiterhin noch Angaben zur Höhe und Breite notwendig. Zentraler Ausgangspunkt ist dabei der Hauptspant mittschiffs (midship frame).

Die Oberauflangerlinie (Top-Timber Line, TTL) beschreibt die Höhe des Schiffrumpfs an den einzelnen Spanten.[vi]

Am Hauptspant (in den Plänen durch Å gekennzeichnet) erreicht die sich daraus ergebene Kurve ihren tiefsten Punkt (lowest place or midships, Punkt ‚P’ der Kurve FPK in Abb. 2).

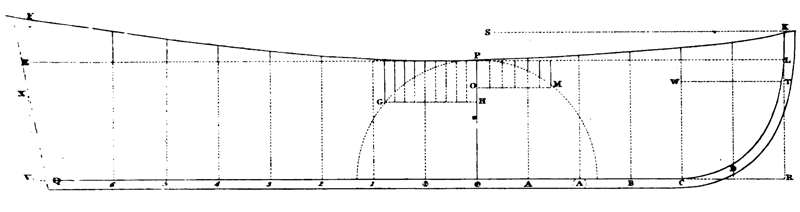
Top Timber Line, Konstruktionswasserlinie

Abbildung 2

Die proportionale Seitenhöhe in Punkt P (Height of the Top-Timber Line) läßt sich für die vorherrschenden Schiffstypen im 18. Jahrhundert nach folgender Regel annäherungsweise berechnen:

Für Kriegsschiffe mit drei Geschützdecks beträgt die Höhe der Oberauflanger an der niedrigsten Stelle bzw. mittschiffs ⁷/₃₀ der Länge (s.o.), bei Zweideckern und kleineren Schiffen ¹/₅ der Länge und bei Kauffahrern ⁵/₂₃ der Länge des Unterdecks.[vii]

Besonders die letzte Methode stellt keine verbindliche Regel dar, sie basiert wie die anderen auf Durchschnitts- bzw. Erfahrungswerten und ist in ihren Ergebnissen stets in Abhängigkeit zu den generellen Abmessungen zu betrachten bzw. daran anzupassen.[viii]

Der französische Physiker und Astronom Pierre Bouguer äußert sich in seinem Werk Traité du Navire von 1746 zur nachträglichen Bestimmung des Massenmittelpunkts (Center of Gravity) eines bereits gebauten Schiffs ähnlich wie bereits Ollivier über die mangelnde wissenschaftliche Arbeitsweise der Konstrukteure im 18. Jahrhundert:

„Allerdings zeichnen die Baumeister immer eine Wasserlinie in ihre Entwurfsskizzen ein, um die exakte Größe der Wasserverdrängung zu ermitteln, wenn das Schiff voll beladen ist; es ist aber ebenfalls wahr, daß sie über keine zuverlässige Methode verfügen, diese zu bestimmen, und ignorieren vollkommen die unterschiedliche Verdrängung des Wassers vorn und achtern.“[ix]

Deswegen überrascht es auch wenig, in der entsprechenden Literatur nur vage Aussagen zu dieser Thematik zu finden. Selbst Henri Louis Duhamel du Monceau legt am Beispiel eines 70-Kanonen-Schiffs den Ausgangspunkt, von dem aus die Load-Water Line in den Seitenriß eingezeichnet wird, 2ft 7in 6ln (was ¹/₈ der Höhe des Geschützdecks mittschiffs entspricht) unterhalb des Großdecks am Hauptspant fest.[x] Wie diese Größe ermittelt wird, oder ob es sich dabei ebenfalls um einen Erfahrungswert handelt, bleibt leider unerwähnt.

Eine ähnliche Formel findet sich in The Shipwright’s Vade-Mecum von David Steel. Demnach läßt sich die Höhe der Konstruktionswasserlinie (Height of the Load-Water Line) folgendermaßen errechnen:

Die Höhe der Konstruktionswasserlinie beträgt in Dreideckern ¹²/₂₃ oder etwas mehr als die Hälfte der Höhe der Oberauflangerlinie, in Zweideckern ³/₅ der der Höhe Oberauflangerlinie und in anderen Schiffen normalerweise ⁵/₈ der Höhe der Oberauflangerlinie am niedrigsten Punkt (Hauptspant). Die Höhe der Konstruktionswasserlinie ist dabei von der Unterseite des Kiels aus zu bemessen.[xi] Auch die von Steel genannten Methoden sind nur als annäherungsweise Lösungen, Approximationen, zu verstehen.

Anhand einiger Beispiele soll die Tauglichkeit dieser Regeln gezeigt werden (s. Anhang).

Beispiele:

Die Berechnungen nach Steel wurden an Kopien von Originalplänen der Admiralty Collection des National Maritime Museums durchgeführt, soweit verfügbar.

Verzerrungsfehler in bezug auf die Seitenverhältnisse/korrekte Größe können durch den Reproduktionsprozeß (Digitalisierung, Bearbeitung, Ausdruck) nicht ausgeschlossen werden.

Zu den Beispielen:

Erstes Objekt zur Überprüfung der o.g. Methoden ist die Victory. Es dürfte wohl kaum ein bekannteres Schiff aus dieser Zeit geben. Das Design stammt aus der Feder von Thomas Slade und ist auf dessen Triumph-Klasse (74) zurückzuführen, welche die Konstruktionsweise der französischen Prise L’Invincible nachbildet. Die ermittelten Werte für die TTL und LWL stimmen mit den Plänen (leider keine Originale) nahezu 1:1 überein.

Zweites Beispiel ist die Mars nach Plänen von Sir John Henslow. Auch hier entsprechen die errechneten Höhen denen der Konstruktionszeichnungen.

Als drittes Modell dient die Sloop Pelican, die ursprünglich als Kauffahrer gebaut und erst einige Jahre später von der Royal Navy angekauft wurde. Sie stammt aus einer Werft in Shoreham (nahe Brighton), nähere Angaben zum Design fehlen. Die berechneten Maße stimmen mit vernachlässigbar geringen Abweichungen ebenfalls mit denen des Bauplans überein.

Weitere Prüfungsbeispiele: HMS Neptune (1791), HMS Swiftsure (1804), HMS Thunderer (1783); Ardent-Class: HMS Raisonnable (1768), HMS Agamemnon (1782); HMS Sirius (1797), HMS Surprise (Unité, 1794), HMS Unicorn (1748).

Literaturverzeichnis:

Bell, Andrew (Hrsg.)/Macfarquhar, Colin et al.: Encyclopaedia Britannica, 3^rd ed., Vol. XVII, Edinburgh 1797.

Goodwin, Peter: Nelson’s Victory, 101 Questions & Answers about HMS Victory, London 2006.

Murray, Mungo(Hrsg.)/Henri Louis Duhamel du Monceau: A Treatise on Ship-Building and Navigation, London 1764.

Nowacki, Horst: Developments in Fluid Mechanics Theory and Ship Design before Trafalgar; zum Kongreß “Technology of the Ships of Trafalgar” von Madrid und Cadiz (3. bis 5. November 2005), Madrid 2006.

Steel, David: The Shipwright’s Vade-Mecum, London 1805.

Welch, John Joseph: A Text Book of Naval Architecture, London 1891.

Winfield, Rif: British Warships in the Age of Sail 1714-1792, Barnsley 2007.

[i] Steel, The Shipwright’s Vade-Mecum, 157; Murray/Duhamel, The Elements of Naval Architecture, 33.

[ii] Steel, a.a.O., 157.

[iii] Nowacki, Developments in Fluid Mechanics Theory and Ship Design before Trafalgar, 33f.

[iv] Welch, A Text Book of Naval Architecture, 9.

[v] Steel, a.a.O., 162.

[vi] Bell/Macfarquahr et al., Encyclopaedia Britannica, Ship-Building, 378.

[vii] Steel, a.a.O., 164.

[viii] Steel, a.a.O., 164.

[ix] Murray, The Elements of Naval Architecture, Extracts from M. Bouguer’s Traité du Navire, 41.

[x] Murray/Duhamel, a.a.O., 18.

[xi] Steel, a.a.O., 164.